Englands Gesamttodesraten nach Impfstatus wörtlich genommen

2021-12-31

Frank Siebert

Den Daten des britischen Office for National Statistics (ONS), veröffentlicht unter dem Titel ""Deaths by vaccination status, England" ¹ , wurden große Aufmerksamkeit geschenkt, weil Daten dieser Art praktisch nirgends sonst auf der Welt verfügbar sind. In Deutschland ist mir keine ähnliche Datenquelle bekannt.

Ich habe in einem früheren Artikel bereit auf die Arbeit von Norman Fenton und Martin Neil an diesen Daten hingewiesen ² .

Doch folgen Sie mir doch in die Tiefen dieser Daten. Schauen wir uns an, was uns diese Daten sagen, wenn wir sie wörtliche nehmen.

Schlussfolgerungen

Die Daten aus dem Office for National Statistics über die Gesamtsterblichkeit in England aufgeschlüsselt nach dem Impfstatus macht die folgenden interessanten Aussagen:

• Die Impfungen erhöhen die Gesamtsterblichkeitsrate der Ungeimpften.
• Es ist möglich die erste und die zweite Impfung in der gleichen Woche zu erhalten.

Dies, ich möchte dies Betonen, ist keine Aussage von mir. Es ist eine Aussage, welche in die Daten des Office for National Statistics einkodiert ist. Ich betone explizit, dass ich nicht an die Wahrheit dieser Aussagen glaube.

Im Folgenden können Sie mich bei meinen Untersuchungen der Daten begleiten, um mit mir zusammen diese zwei Ausssagen aus diesen heraus zu schälen. Ganz am Ende komme ich zu anderen Schlussfolgerungen, fühlen Sie sich frei Ihre eigenen zu ziehen.

Die Untersuchung der Daten

Auf dem Reiter 4 der zur Verfügung gestellten Excel-Datei werden die Gesamtsterblichkeitsdaten mit folgenden Spalten aufgeschlüsselt: "Week ending" (Datum des Endes der Woche), "Week number" (Kalenderwoche), "Vaccination status" (Impfstatus), "Age Group" (Altersgruppe), "Number of deaths" (Anzahl der Todesfälle), "Population" (Gruppengröße), "Death rate per 100,000" (Todesrate je 100.000), "Lower conficence limit" (Untere Grenze der vermuteten Genauigkeit), "Upper confidence limit" (Obere Grenze der vermuteten Genauigkeit).

Mit ein wenig Pech übersehen Sie vielleicht die eine Spalte, welche ohne eine Benennung daher kommt, welche in einigen Zeilen die Markierung 'u' für "unsicher" aufweist. Das Kriterium für diese Markierung wäre vermutlich von Interesse, aber es ist nicht in den Erläuterungen unter der Tabelle erklärt. Aus der Position der Spalte erschließt sich, dass sie sich auf die Todesrate je 100.000 bezieht, genauso wie die beiden Spalten mit den Konfidenzgrenzen.

Wir lernen aber aus der Dokumentation unter der Tabelle: ''Die Zahlen basieren auf vorläufigen Sterbedaten und dem Public Health Data Asset (PHDA), ein verknüpfter Datensatz von Personen wohnhaft in England, welche mit der Volkszählung 2011 und dem GP Patienten Register verknüpft werden konnten.

Die Tabelle bietet die Daten in 4 Altersgruppen und 4 Impfstatusgruppen unterteilt an, mit den Altersgruppen '10-59', '60-69', '70-79 und '80+', und den Impfstatusgruppen 'Unvaccinated' (Ungeimpft), 'Within 21 days of the first dose' (Bis 21 Tage nach der der ersten Dosis), '21 days or more after first dose' (21 oder mehr Tage nach der ersten Dosis) und 'Second dose' (Zweite Dosis).

Warum das ONS entschied nur eine große Altersgruppe für die 10 bis 59 jährigen Personen zu verwenden bleibt mir ein Geheimnis. Es hätte das Leben ungezählter Statistiker deutlich vereinfacht, wenn die Altersgruppen jenen entsprächen, welche für die Verfolgung des Impfvortschritts verwendet wurden.

(Nachtrag zur deutschen Fassung: Inzwischen habe ich herausgefunden, dass die Altersgruppen für die Verfolgung der Anzahl der Impfungen über die Zeit hinweg in den Reports des ONS feingliedriger wurden. Die Daten sind nach Tag und nach Woche aufgeteilt erhältlich, so dass in früheren Imfzeiträumen nur über 80 und unter 80 unterschieden werden kann, wärend in den Datensätzen neuerer Wochen oder Tage Altergruppen von 5 Jahren Breite unterschieden werden. Wie Statistiker aus diesen Zahlen den Verlauf des Impffortschritts einzelner Altersgruppen über den gesamten Zeitraum ermitteln können sollen, ist mir völlig unklar. Nachtrag Ende)

Gegenüberstellung der berechneten altersspezifischen Todesraten und der angegebenen Todesraten

Für das Zählen von Todesfällen getrennt nach Impfstatus und Altersgruppe und der Berechnung einer Todesrate als Quotient der Todesfälle geteilt durch die Gruppengröße würden Sie eigentlich kein Konfidenzintervall benötigen, wenn Sie diese Zahlen kennen.

Kennen Sie diese Zahlen aber nicht durch Zählen, oder wenn Sie die Zahlen nicht genau kennen, würden Sie dann nicht ein Konfidenzintervall für jede Zahl getrennt angeben, bei welcher Sie sich nicht sicher sind? Können wir mehr über die Quelle dieser Konfidenzintervallgrenzen und der "unsicher"-Markierungen heraus finden?

Lassen Sie uns ein paar Zeilen verwenden um eine selbst errechnete Todesrate mit der angegebenen Todesrate zu vergleichen. Am 4. Juni wurden in der ungeimpften Altersgruppe '10-59' 125 Todesfälle registriert und die Gruppengröße bestand aus 11.832.842 Personen.

Um die Todesrate je 100.000 zu errechnen multiplizieren wir einfach 125 mit 100.000 und teilen dies durch 11.832.842.

125*100,000/11,832,842 = 1.056381

Gerundet auf eine Stelle hinter dem Komma erhalten wir genau das Ergebnis, welches in dem Datenblatt ebenfalls angegeben ist. Wir sollten aber ein Beispiel wählen, in dem wir mehr als zwei Stellen vergleichen können, es spielt keine Rolle, ob diese vor oder nach dem Komma sind, um eine bessere Auflösung bei unserem Vergleich zu erhalten.

Der Eintrag der ungeimpften 80+ Todesfälle am 4. Juni scheint hierfür geeignet zu sein, er ist auch nicht als "unsicher" markiert.

209*100,000/75,045 = 278.499566

Auch für diese Zeile erhalten wir exakt das Ergebnis, welches auch in dem Datenblatt angegeben ist. Dies ist der Punkt, an dem es vielleicht sinnvoller ist das Programm zu verwenden, vor dem wir sitzen, um diesen Vergleich für alle Zeilen zu machen, um eventuell vorhandene Abweichungen zu finden.

Machen Sie dies, so finden Sie, dass alle selbst errechneten Todesraten mit den angegebenen übereinstimmen, außer bei einigen Zeilen, in denen keine Todesrate vom ONS angegeben wird. In einigen anderen Zeilen finden sich exakt die berechneten Raten, allerdings mit der "unsicher"-Markierung daneben, was vielleicht mit einer zu klein werdenden Gruppengröße zusammen hängt.

Die "unsicher"-Markierung wirft Fragen auf. Sie mag oder mag nicht mit dem Konfizenzintervall zusammen hängen, aber ich habe diese Information bisher nicht in der Dokumentation gesehen. Was wir immerhin bei unserer Untersuchung heraus fanden: Die Todesraten wurden offensichtlich nicht durch weitere Informationen beeinflusst. Sie sind wirklich mit den Angaben des Datenblattes mit einfachster Mathematik errechnet

Ein Blick auf den Gruppenwechsel

Was passiert zur Zeit der Impfungen mit den Todesraten?

Um uns dies Anzuschauen verwenden wir zunächst die Todesraten zweier benachbarter Gruppen und lassen uns dazu weniger prominent die Veränderungen der Gruppengrößen anzeigen, welche Aufschluss über den Impffortschritt geben, während sie zu geringerem Maße auch Veränderungen durch Todesfälle enthalten. Da dieser zweite Aspekt allerdings nicht dominiert, ignorieren wir diesen zunächst.

Wir beginnen unsere Sichtung mit der Altersgruppe 70 bis 79, weil die Altersgruppe 80+ mit den Impfungen bereits im Jahr 2020 begann, und daher nicht die vollständige Sicht auf das Szenario gibt. Wir beginnen nicht mit der Altersgruppe 10 bis 59, weil diese Gruppe viel zu groß ist und sich die Impffortschritte der unveröffentlichten Untergruppen über eine lange Periode verteilt.

Die Altersgruppe 70 bis 79 als eine schmale Altersgruppe zwischen zwei weiteren schmalen Altersgruppen ist die perfekte Wahl für den Start.

Grafik 1

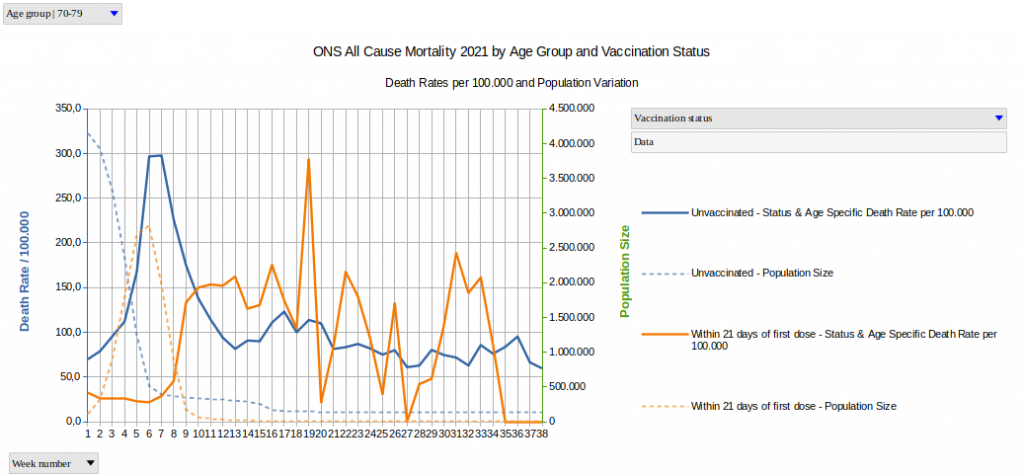
Diese Grafik erklärt uns, dass die Todesrate der Ungeimpften in sehr guter Annäherung der Gruppengröße der "Bis 21 Tage nach der ersten Dosis"-Gruppe folgt.

Wenn Sie dies irritiert, dann sind Sie damit nicht alleine.

Wenn wir dieses Ergebnis wörtlich nehmen, dann müssen wir die Behauptung aufstellen, dass die erste Dosis der Impfung die Ungeimpften tötet.

Die wilden Ausschläge der Todesrate der "Bis 21 Tage nach der ersten Dosis"-Gruppe, welche um die Kalenderwoche 17 starten, ergeben sich Aufgrund der geringen Gruppengröße. Sie können diese ignorieren.

Wenn wir dieses Ergebnis nicht wörtlich nehmen, dann müssen wir darüber nachdenken: Was ist an diesen Daten falsch?

Drei mögliche Erklärungen für einen Effekt, wie wir ihn hier sehen, wurden von Norman Fenton, Professor for Risk Information Management, und Martin Neil, Professor for Computer Science and Statistic, gegeben. Beide lehren an der Queen Mary Universität in London und stellten auf der Basis der Daten die Frage "Is vaccine efficacy a statistical illusion?" ³ .

Ihre drei möglichen Erklärungen waren:

1. Eine Verzögerung in der Meldung von Todesfällen könnte verantwortlich sein, was in einer schrumpfenden Gruppe zu einer Erhöhung der Todesraten führt, welche umgekehrt zum Schrumpfen der Gruppengröße verläuft. Offiziell kann diese Erklärung nicht zutreffen, da das ONS erklärt die Angaben zum Todestag und nicht den Tag der Todesmeldung zu verwenden.
2. Die Gruppengröße der Ungeimpften wurde vielleicht unterschätzt, was ebenfalls zu einer erhöhten Todesrate in einer Schrumpfenden Gruppe führen würde.
3. Todesfälle wurden vielleicht falsch kategorisiert, also geimpfte Todesfälle als ungeimpfte Todesfälle gezählt.

Am Ende sind wohl auch andere Erklärungen möglich, oder eine Kombination von Erklärungen. Wir kennen die Erklärung jetzt noch nicht, aber wir wissen, dass etwas mit diesen Daten nicht in Ordnung ist, denn wir müssen einfach glauben, dass Ungeimpfte nicht an den Impfungen anderer sterben. Die Daten, wie wir sie hier sehen, verlangen nach einer Erklärung. Zu Behaupten es sei wahr, dass Ungeimpfte sterben weil andere ihre Impfung erhalten, beleidigt unseren gesunden Menschenverstand.

Wir haben ein Artefakt in diesen Daten gefunden, welches definitiv einen Effekt aufzeigt, den es im echten Leben nicht gibt. Da wir die Ursache für dieses Artefakt nicht kennen, erscheint es auch nicht möglich dieses sicher aus den Daten zu entfernen. Aber vielleicht ist es ja möglich, lassen Sie uns tiefer hinein schauen.

Todesraten getrennt nach Altersgruppe

Für die weitere Analyse habe ich PostgeSQL installiert ⁴ und ein paar SQL Views geschrieben. Auf diese Weise ist am Besten dokumentiert, was der jeweilige View genau macht um die hier gezeigte Grafik zu produzieren ⁵ . Die Links auf die jeweilige Dokumentation finden Sie im Schriftartikel.

Grafik 2

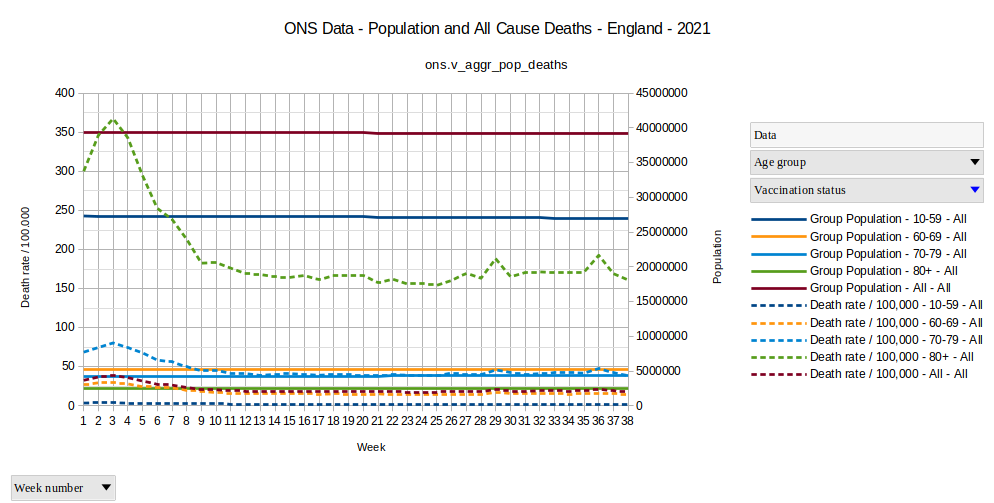
Diese Grafik zeigt uns, dass in der impfstatus-unabhängigen Gesamttodesrate nichts besonderes passiert. Die höchste Todesrate in allen Altersgruppen ist in der Kalenderwoche 3, was darauf hinweist, dass dies nichts mit den Impfungen zu tun hat, sondern eine einfache saisonale Erhöhung ist, wie sie im Winter üblich ist.

Es ist auch weder für die COVID Todesfälle noch für die Impftodesfälle zu erwarten, dass sie sich hier Dominat zeigen, und die Gesamttodesrate war bereits am Sinken, als sich die seltsamen Erhöhungen der Gesamtsterblichkeit der ungeimpften Gruppe in den ONS Daten zeigt.

Dies kann als weiterer Indikator dafür gesehen werden, dass der seltsame späte Anstieg der Todesfälle in der ungeimpften Gruppe ein nur statistischer Effekt ohne reale Relevanz ist.

Die Todesraten - Inokulierte versus Nicht-Inokulierte

Ich werde in der weiteren Vertiefung mich Hauptsächlich auf Altersgruppe 70 bis 79 konzentrieren. Weniger als Vertiefung, sondern weil ich es einfach haben wollte, erzeugte ich auch eine vereinfachte Sicht ⁶ , welche nur zwei Werte für den Impfstatus unterscheidet: Die Gruppe der inokulierten Personen, welche mindestens eine Spritze erhalten haben, und die Gruppe der nicht-inokulierten Personen, welche nie irgend eine COVID-Spritze erhalten haben.

Grafik 3

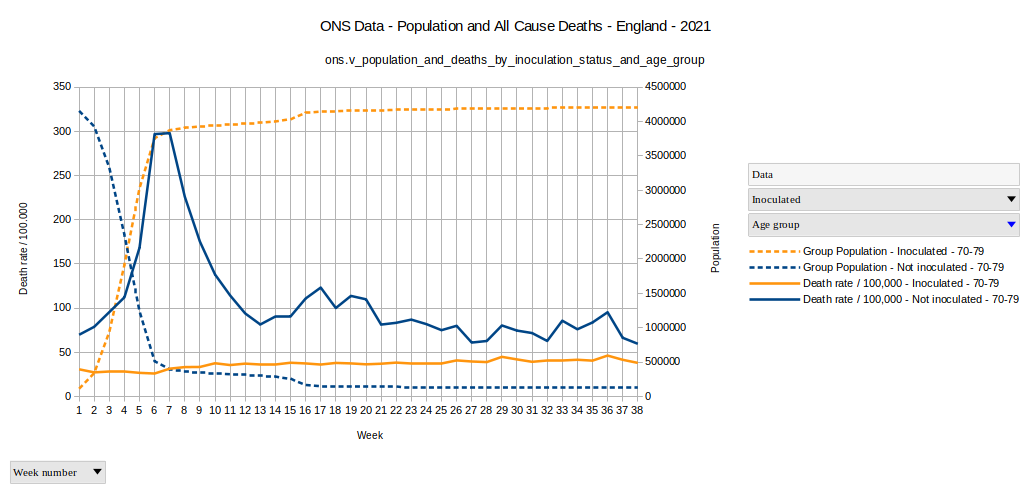
Eine Diskussion der Bedingungen, welche das Entstehen einer solchen Grafik erklären können, in der Impfungen scheinbar zu Todesfällen bei Ungeimpften führt, war - wie bereits erwähnt - von Norman Fenton, Professor for Risc Information Management, und Martin Neil, Professor for Computer Sciences and Statistics, beide an der Queen Mary University in London, in deren Artikel "Is vaccine efficacy a statistical illusion?" ⁷ durchgeführt worden.

Es ist nun meine Absicht mit der Untersuchung weiter zu gehen.

Überprüfung der Gruppen Balance

Das ONS berechnete die Todesraten unter Verwendung der Gruppengröße der Woche und der Todesfälle der Woche. Diese Tatsache kann durch die Kontrollrechnung einiger Zeilen leicht kontrolliert werden, und wir haben dies weiter oben bereits gemacht.

Dies bedeutet, dass die angegebene Gruppengröße der Woche immer die Gruppengröße am Anfang dieser Woche ist.

Wenn wir die Todesfälle von der Gruppengröße abziehen, erhalten die Gruppengröße am Ende der Woche, welche die erwartete Gruppengröße am Anfang der nächsten Woche ist.

Wenn wir keine Altersgruppen hätten, dann wäre dies bereits alles. Aber da wir Altersgruppen haben, können Personen von einer Altersgruppe in eine andere Altersgruppe wechseln, einfach weil sie Geburtstag haben. Für den Start können wir dies zunächst ignorieren, um später auf diesen Punkt zurück zu kommen. Auch die Unterteilung in vier verschiedene Impfstatusgruppen ist für den Start zu kompliziert.

Die nächste Grafik zeigt daher einfach für jede Altersgruppe, um wie viel die Wochen-Ende-Gruppengröße der letzten Woche von der Wochen-Anfang-Gruppengröße der neuen Woche abweicht.

Eine negative Abweichung (unter Null) bedeutet, dass es einen Nettozustrom von Personen durch Geburtstage gab. Eine positive Abweichung (über Null) bedeutet, dass es eine Nettoabwanderung von Personen durch Geburtstage gab. Zumindest ist dies der einzige bekannte Grund in dieser Grafik als Abwanderung aufzutauchen, da die Todesfälle ja bereits in der Berechnung der Wochen-Ende-Gruppengröße eingeflossen sind und in der Differenz vom Erwartungswert daher nicht Auftauchen können. ⁸ .

Grafik 4

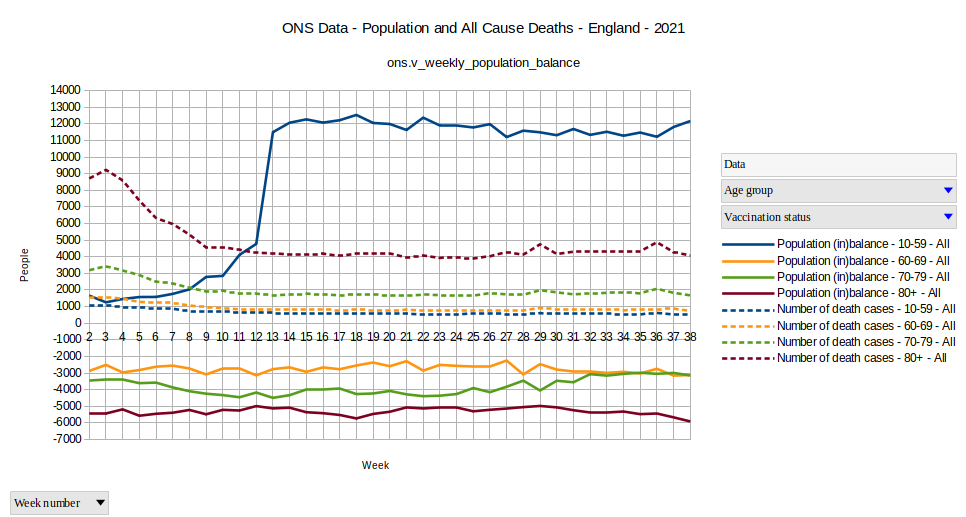
Sieht dies seltsam aus? Was passiert da in der Altersgruppe 10-59 in der Woche 13? Ein Kommentar von Anonymous vom 1. Dezember erklärt, das die Volkszählung 2011 am 27. März beendet wurde ⁹ .

Anders, als ich bisher Annahm, handelte es sich also bis zum 27. März nicht um eine geschlossene Gruppe, da bis zu diesem Datum neue Personen (Kinder) in die Altersgruppe 10-59 durch Geburtstag hinein gelangen konnten. Jetzt weiß ich dies besser als zuvor. Für die Altersgruppe 70-79, auf welcher mein Fokus liegt, spielt dieses Detail allerdings keinerlei Rolle.

Dennoch ist es definitiv gut zu wissen, dass ich mich nicht damit befassen muss, warum bis zum 27.März immer neue Personen in die Betrachtung aufgenommen werden, wo ich doch dachte, es gäbe keine Möglichkeit hierzu.

In dieser Grafik sehen wir, dass eine Menge Personen Woche für Woche die Altersgruppe 10-59 verlassen um in die Gruppe der 60-69 Jährigen zu wechseln. Gleichzeitig wechseln etwas weniger in die Gruppe 70-79, was der Altersgruppe 60-69 eine relativ gleichmäßige negative Abweichung beschert.

Vielleicht sollte ich die Vorzeichen tauschen und einer positiven Abweichung die Bedeutung eines Überwiegens der Zuwanderung geben. Das wäre leicht zu machen, da es sich lediglich um eine Definition handelt. Aber ich bleibe bei der jetzigen Definition und Implementation. Eine Information darüber, ob die Altersgruppe insgesamt wächst oder schrumpft gibt uns diese Sicht sowieso nicht, da die Todesfälle ja nicht mit enthalten sind.

Wir können als nächstes die Abweichungen der ungeimpften und der "Bis 21 Tage nach der ersten Dosis"-Teilgruppen der Altersgruppe 70 bis 79 betrachten.

Grafik 5

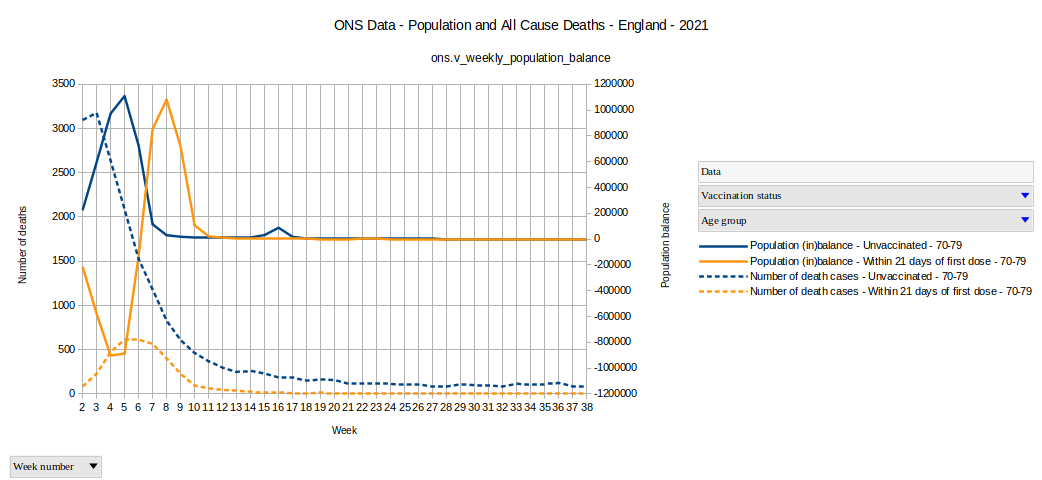
Wir sehen bis zur vierten Woche eine sehr gute Balance, eine Spiegelsymetrie, aber danach verschwindet die Symetrie zwischen den beiden Kurven. Doch dies ist generell Korrekt, da jeder nach 21 Tagen die zweite Gruppe verlassen muss.

Berechnung der Abweichung der 21 Tage-Gruppe

Einfach nur durch optisches Betrachten können wir nicht wirklich sagen, ob die Abweichung der 21 Tage-Gruppe zur Abweichung der ungeimpften Gruppe passt. Da die beiden Abweichungen aber eng miteinander verbunden sind, kann die Abweichung der 21 Tage-Gruppe leicht aus der Abweichung der ungeimpften Gruppe berechnet werden. ¹⁰

Grafik 6

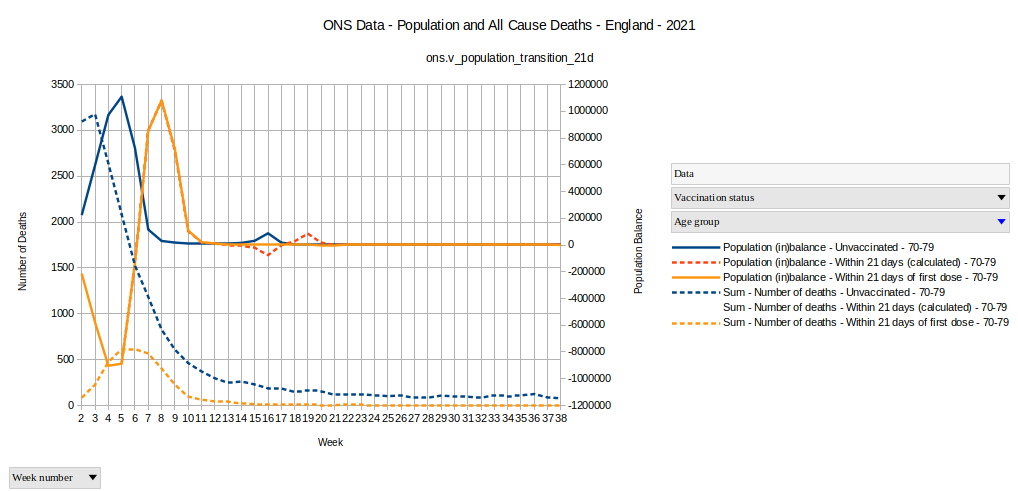
Die gestrichelte rote Kurve ist die berechnete Abweichung, basierend auf der Abwanderung der Personen von der ungeimpften Gruppe. Die orangene Kurve ist die Kurve, welche sich durch den Unterschied zwischen der berechneten Wochen-Ende-Gruppengröße und der in den ONS Daten gemeldeten Wochen-Anfang-Gruppengröße der 21-Tage-Gruppe ergibt.

Die beiden Kurven passen sehr gut zusammen, mit einem anscheinend geringen Unterschied zwischen der 12ten und 21ten Woche. Wenn wir diese Abweichung wörtlich nehmen, dann wurde in diesem Zeitraum entweder ein großer Schwung ungeimpfter Personen geimpft, welche alle zu der Zeit starben und nicht in der Lage waren in die 21 Tage-Gruppe zu gelangen, oder eine ungewöhnlich große Anzahl von ungeimpften Personen hatte Geburtstag in diesen Wochen, so dass sie in der nächst höheren Altersgruppe verschwanden.

Das Ereignis hat seinen Spitzenwert in der Woche 16 und wenn wir in Grafik 4 blicken, dann sehen wir dort keine besonderen Geburtstagsevents in der Altersgruppe 70-79 mit massenhafter Änderung der Altersgruppe wiedergegeben. Und die Variante mit den vielen Todesfällen ist ebenfalls keine Alternative, weil diese registriert worden wären und in dieser Grafik nicht sichtbar würden.

Wir sehen hier Menschen die Gruppe der Ungeimpften verlassen, ohne dass sie in der folgenden Gruppe registriert werden und ohne dass sie als Todesfälle registriert wurden.

Die Konten sind nicht ausgeglichen. Die Buchführung ist nicht sauber.

Aber es ist ja nicht viel, ist es nicht so?

Ein Zoom in die Abweichung im Transit zwischen ungeimpfter und 21-Tage-Gruppe

In Grafik 4 sehen wir die Nettobewegung zwischen den Altersgruppen, nicht ganz direkt, aber wir bekomen eine gute Schätzung.

• Ungefähr 12.000 wechseln jede Woche von der Altersgruppe 10-59 in die Gruppe 60-69
• Ungefähr 9.000 wechseln jede Woche von der Altersgruppe 60-69 in die Gruppe 70-79
• Ungefähr 5.500 wechseln jede Woche von der Altersgruppe 70-79 in die Gruppe 80+

Manchmal ist es etwas mehr oder auch weniger, aber über den Zeitverlauf hinweg ist dies eine recht stabile Situation.

Wir können aber auch mit Blick auf die Altersgruppe 70 bis 79 sagen - es ist eine 10 Jahresgruppe, jedes Jahr mit 365 Tagen, und jeder Tag genauso wahrscheinlich der Geburtstag eines Gruppenmitglieds wie jeder andere dieser Tage. Wir können die wöchentliche Anzahl der Geburtstage, welche Mitglieder in die nächste Gruppe hieven berechnen als:

New ₈₀₊ = Population _70-79 * 7 Tage/Woche / 10 Jahre / 365 Tage/Jahr ¹¹

Wir können diese Berechnung auf Untergruppen der Altersgruppe anwenden, welche ihre Größe Aufgrund von Impf-Ereignissen ändern.

Diese Berechnung gibt uns einen oberen Erwartungswert, in welchem Bereich eine Gruppengrößenänderung in einer Woche in etwa ausfallen kann, ohne Verdächtig zu wirken. Es ist ein großzügiger Grenzwert, denn:

• Es wird erwartet, dass die am meisten gefährdeten älteren Personen in größerem Umfang früher geimpft wurden, was Geburtstagsevents im ältesten Jahrgang der ungeimpften Untergruppe weniger wahrscheinlich macht als im Durchschnitt der Altersgruppe.
• Die ungeimpften, welche aus der nächst jüngeren Altersgruppe hinzukommen könnten, werden nicht mit betrachtet. Diese Betrachtung würde die Grenzwerte einengen.

Genau anders herum wäre die Betrachtung korrekt für die 21 Tage Gruppe dieser Altersgruppe. Deren Geburtstagsevents würden die Grenzen der Erwartung in genau entgegengesetzter Richtung schmälern oder verbreitern. Da allerdings die Signal sendende Gruppe die ungeimpfte ist, beschränken wir uns zunächst auf deren Betrachtung, einfach das dreifache der Grenzwerte nehmend, um auf der sicheren Seite zu sein. Wenn wir den Eindruck erhalten, dass eine genauere Betrachtung wichtig ist, dann können wir die zusätzlichen Aspekte später hinzufügen.

In der folgenden Grafik zeigen die gestrichelten Kurven den oberen und unteren Grenzwert für die maximal erwarteten geburtstagsbedingten Abweichungen in der wöchentlichen Abweichung der Gruppengröße, basierend auf der Größe der ungeimpften Gruppe in der Altersgruppe 70-79.

Grafik 7

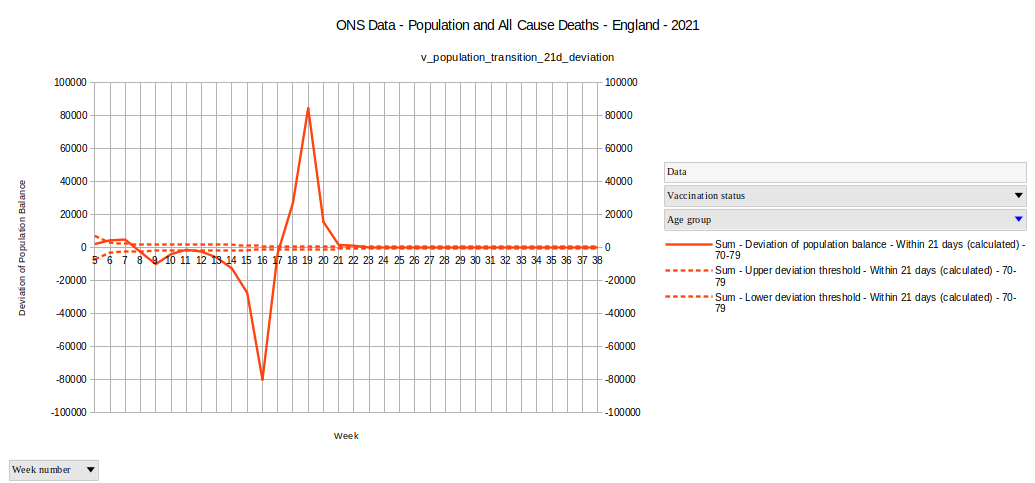
Wir sehen ein ziemlich starkes Signal in dieser Darstellung, weit außerhalb der erwarteten geburtstagsbedingten Effekte. In der Kalenderwoche 16 übersteigt die Abweichung der Gruppengrößenänderung die erwarteten geburttagsbedingten Effekte um etwa 80.000 Personen.

Was ist denn nun die exakte Bedeutung dieses Signals?

Ungefähr 120.000 Personen verließen die ungeimpfte Gruppe dieser Altersgruppe während der Wochen 14, 15 und 16 ohne Mitglied in der 21-Tage-Gruppe zu werden. Ein möglicher Transfer in die Altersgruppe 80+ kann dies nicht erklären. Der Blick auf Grafik 4 zeigt uns deutlich, dass diese 120.000 in diesen 3 Wochen nicht in die Altersgruppe 80+ wechselten.

In Grafik 2 sehen wir in der Woche 16 einen deutlichen Anstieg in der Gruppe der Inokulierten, synchron mit einer Reduzierung der Gruppe der Nicht-Inokulierten. Dies bedeutet möglicherweise, dass der größere Teil dieser 120.000 Personen in eine andere Gruppe wechselte. Die Frage bleibt bestehen: In welche Gruppe wechselten sie?

Auf der Such nach der Transfer-Zielgruppe der 120.000 Personen

Da ein Wechsel in die Altersgruppe 80+ definitiv nicht für diese 120.000 Personen verantwortlich gemacht werden kann, müssen wir unseren Blick auf die weiteren Gruppen in der Altersgruppe 70-79 richten.

Grafik 8

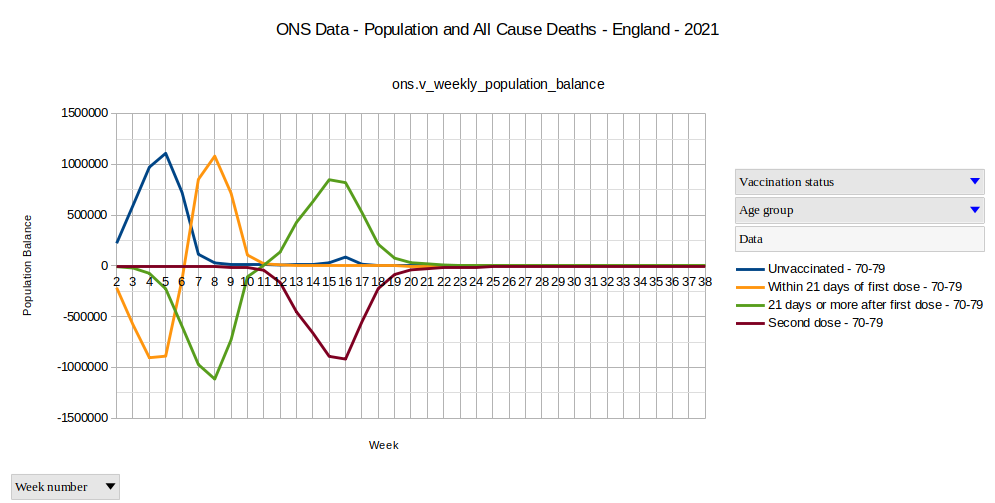
Nun, da unser Blick durch die bis zu diesem Punkt vorgenommenen Datenanalysen geschult wurde, können wir unmittelbar sehen, dass zumindest der größere Teil dieser 120.000 ungeimpften Personen direkt in die Gruppe der zweifach Geimpften wechselte. Können Sie es sehen?

Ungefähr 120.000 Personen wechselten in den Kalenderwochen 14, 15 und 16 direkt von der ungeimpften in die zweifach geimpfte Gruppe.

Sie dürfen mich nicht Fragen wie dies möglich ist. Ich formuliere nur eine Aussage, welche durch den Gesamttodesfälle-Datensatz aus dem Office of National Statistics gemacht wird. Es ist nicht meine eigene Aussage, es ist eine Aussage, welche durch die Daten selbst gemacht wird.

Ein möglicher Grund drängt sich auf: Vielleicht wurden sie mit dem Janssen / Johnson&Johnson Einfachdosis-Impfstoff geimpft?

BBC berichtet am 28. May: "Janssen single-dose Covid vaccine approved by UK" ¹² .

Dies ist das Ende der Kalenderwoche 21, welche viel später war. Die Einfachdosis-Impfung kann also keine Erklärung anbieten.

Im Nachgang

75.884 Todesfälle insgesamt wurden für die Altersgruppe 70-79 in dem vom ONS Datensatz abgedeckten Zeitraum gemeldet.

Wenn wir nicht glauben, dass die Impfungen verantwortlich für den Tod Ungeimpfter sind, und wenn wir nicht glauben, dass manche Menschen beide Dosen innerhalb einer Woche erhielten, was erheblich von dem offiziellen Impfplan abweichen würde, was ist dann die abschließende Schlussfolgerung?

Ungefähr 120.000 Ungeimpfte erhalten plötzlich ihre zweite Dosis, wärend die Gesamtzahl der Todesfälle in der gleichen Altersgruppe weniger Personen umfasste.

Ich kann nur die Feststellung machen, dass die komplette Anzahl der Todesfälle in diesen 120.000 Personen verschwinden kann, welche plötzlich zwei Übergangsgruppen überspringen.

Und diese, so muss ich ebenfalls feststellen, waren die überlebenden sogenannten "Ungeimpften". Ich muss sie nun "sogenannte Ungeimpfte" nennen, weil sie offensichtlich Geimpft waren und die Impfung überlebten bis sie die zweite Dosis erhielten.

Niemand kann uns sagen, wie viele nicht überlebende sogenannte "Ungeimpfte" vor der zweiten Impfung starben, und so die offizielle Todesrate der ungeimpften Gruppe erhöhten.

Betrachten wir erneut das Phänomen, dass die Todesrate der Ungeimpften scheinbar für ihren besseren Teil ihres Verlaufes der Gruppengröße der "Bis 21 Tage nach der ersten Dosis"-Gruppe folgt, wie es in Grafik 1 zu sehen ist. Nun, da wir um die 120.000 - in Gänsefüßchen - "Ungeimpfte" in den Wochen 14, 15 und 16 ihre zweite Dosis erhalten sehen, ist es viel mehr als nur eine Vermutung, dass diese Todesrate der - in Gänsefüßchen - "Ungeimpften" von geimpften Dominiert wird, welche fälschlich als Ungeimpft gezählt wurden.

120.000+ Personen im Alter von 70 bis 79 wechselten nicht in die Gruppe 'Bis 21 Tage nach der ersten Dosis" nachdem sie ihre erste Dosis erhielten.

Dies sagt uns auch: Jede einzelne Todesrate, welche für die "Ungeimpften" der Altersklasse 70 bis 79 in den ONS Daten angegeben wurde, verdient die Kennzeichnung als "unsicher".

Tatsächlich ist offensichtlich das Gleiche auch für alle anderen Todesraten in der Altersgruppe 70 bis 79 wahr.

Das Office for National Statistics hat nicht geliefert, was es versprochen hat.

Bieten Sie mir eine andere zufriedenstellende Schlussfolgerung an, Bitte.

Weiter Gehen?

Da das Thema dieser Statistik, zusammen mit der Wahl für eine wohl-definierte geschlossene Gruppe, aus sich selbst heraus eine Art doppelter Buchführung in den Daten etabliert, war es möglich eine Diskrepanz in den Daten zu identifizieren, welche eine fehlerhafte Buchführung nachweist.

Dank der Natur der doppelten Buchführung mag es noch immer möglich sein, die existierenden Fehler in dieser Buchführung zu einem gewissen Maße zu korrigieren. Vielleicht, wenn sich dies als machbar herausstellt, werde ich weitere Einsichten hierzu in einem späteren Artikel anbieten.

Erkenntnisse haben immer vorläufigen Charakter und sind immer individueller Natur . Sie selbst entscheiden, ob Sie Erkenntnisse anderer als Meinung übernehmen oder ob Sie sich Erkenntnisse selbst erarbeiten. Meine Quellenangaben sollen Ihnen bei letzterem eine Hilfestellung geben, Sie sollten aber immer auch weitere Quellen verwenden.

Glauben Sie nicht, auch nicht mir, sondern prüfen Sie und schlussfolgern Sie selbst.

Fußnoten

Kategorie:Deutschland Kategorie:England Kategorie:COVID-19